Put the 4 pieces forming a central circle.
Now put the pieces so that the pieces of circle touch the vertices of the frame.
How do you explain that the central square is missing?


Explanation
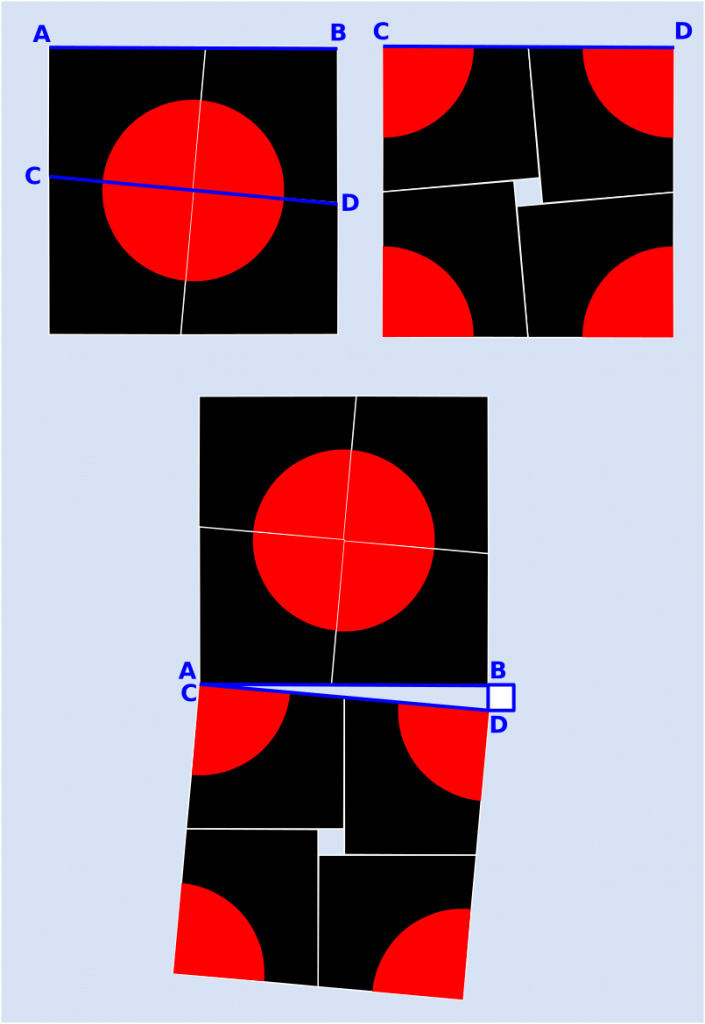
Pots comprovar que les 4 peces, en la segona posició, no ballen tant dins el seu marc com amb la primera posició. El segment CD que uneix els dos costats de forma inclinada és lleugerament més llarga que el segment AB, costat del quadrat en la primera posició,
The sides of the two pieces that form the CD line inclined to the first position, are the ones that in the second position are forming the outside of the square.
- Hotel Area: Sala Pere Puig Adam
- Minimum age: from 6 years old.
- Required time: 5 minutes.
- Number of participants: One or more people
- Keywords: Pythagoras, puzzle
- Taxonomy: Geometry
The difference between AB and CD, is almost imperceptible, this is precisely what causes surprise.
But the difference in surfaces between the AB side square and the CD side, it is appreciable, is the missing square.
To see what this square is like, we use the Pythagoras theorem. The rectangle triangle drawn in blue on the figure shows the construction that you can also see in the Pythagoras module.
The square on CD is the sum of the square on AB and the square on the small side.
