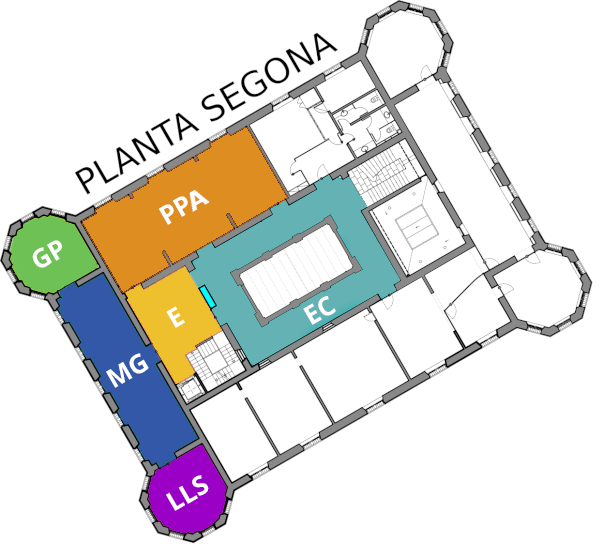
segona planta
Sala Pere Puig Adam
Geometria, corbes, poliedres i fórmules inductives
Aquesta sala situada enfront de l’escala i l’ascensor està dedicada a la geometria tant plana com 3D, les corbes i les fórmules inductives.
Qui era Pere Puig Adam ?
Pere Puig i Adam (Barcelona, 1900 – Madrid, 1960) fou un pedagog, matemàtic i enginyer.
A més dels seus treballs de recerca modelitzant matemàticament problemes sorgits de la física, com a professor de matemàtiques va escriure importants llibres de text tant en l’àmbit universitari com secundari. Les seves idees avançades al seu temps són encara avui un referent com podeu comprovar llegint el seu decàleg de 1955.
Decàleg de l'ensenyament de les matemàtiques de Pere Puig Adam (1955)
- No adoptar una didàctica rígida, sinó adaptada en cada cas a l’alumne, observant-lo constantment.
- No oblidar l’origen concret de la Matemàtica ni els processos històrics de la seva evolució.
- Presentar la Matemàtica com una unitat en relació amb la vida natural i social.
- Graduar acuradament els plans d’abstracció.
- Ensenyar guiant l’activitat creadora i descobridora de l’alumne.
- Estimular aquesta activitat despertant interès directe i funcional vers l’objecte del coneixement.
- Promoure en tot el possible l’autocorrecció.
- Aconseguir un cert mestratge en les solucions abans d’automatitzar-les.
- Cuidar que l’expressió de l’alumne sigui traducció fidel del seu pensament.
- Procurar a qualsevol alumne èxits que evitin la seva desmoralització.
Alguns mòduls d'aquesta sala
Les corbes que s’obtenen fent rodar circumferències de diferent mida.
Mira les seccions dels objectes il·luminades pels leds vermells d’aquesta anella.
Comprova com es poden aconseguir enrajolats diferents amb la mateixa rajola.
Tres anelles per enllaçar-les d’una forma molt especial.
Prova de posar el tetraedre i l’octaedre dins el cub.
Visualitzant propietats numèriques amb cubs i altres peces.
Proposta de transformació d’una figura a una altra movent tan sols una peça per completar un recorregut circular.
Dos triangles iguals, de colors diferents per cada costat, no simètrics. Un d’ells està dividit en tres parts les quals sí que són simètriques. Es proposen 4 reptes consistents en la seva col·locació en els corresponents espais.
El con artesanal de fusta que mostra les seves seccions: Circumferència, el·lipse, paràbola i hipèrbola.
Amb les mateixes peces, reconstrueix dos polígons.
Amb 5 triangles cal construir 1,2 i 3 triangles equilàters
Un octaedre i 20 tetraedres amb cares imantades i una proposta de construcció de l’ Stella octangula i el cub
Un pentàgon girant que funciona com un engranatge on les dents han desaparegut
Aparell articulat que mostra la transformació del pla anomenada inversió geomètrica que transforma rectes en circumferència. Resseguint amb una punta les siluetes de rectes i circumferències es comprova com l’altra punta traça les figures corresponents.
Un enrajolat amb tessel·les en forma de sargantana ideades per l’artista M. Escher.
Construeix poliedres amb peces imantades.
Aixequem aquests arcs amb coixins.
Com canvien les longituds, superfícies i volums d’objectes semblants?
Amb totes les peces construïm 3, 2 o 1 triangles equilàters
Posa els bastons blaus, perpendiculars a les arestes del dodecaedre per construir l’icosaedre.
Múltiples formes de visualitzar i entendre aquest famós teorema
Les quatre peces poden posar-se al marc de dues formes, d’una, omplen el marc i d’una altra deixen un petit quadradet central.
Amb 64 cubs transparents es proposa construir un cub 4x4x4 amb un recorregut continu.
Dues boles, una baixa en línia recta, l’altre fent corba. Quina arriba abans?
Recursos i material addicional
- Dossier per treballar en aquesta sala preparat per Toni Gomà i Daniel Bosch
- Fitxes didàctiques de Marina Agudelo, 7 corresponen a mòduls d'aquesta sala
- Fitxes didàctiques dels companys d'ADEMGI, 4 corresponen a mòduls d'aquesta sala.
- Article de Josep Rey i Manel Udina al NouBiax 38 sobre el mòdul de fòrmules inductives.
- Article d'Anton Aubanell al NouBiax 39 sobre el mòdul "Perímetre, superfície,volum"